Chapter 5 Support Vector Machines
Hands-On Machine Learning with Scikit-Learn, Keras & Tensorflow 2nd Edition by A. Geron
A Support Vector Machine (SVM) is a powerful and versatile Machine Learning model, capable of performing linear or nonlinear classification, regression, and even outlier detection.
It is one of the most popular models in Machine Learning, and anyone interested in Machine Learning should have it in their toolbox.
SVMs are particularly well suited for classification of complex small- or medium-sized datasets.
This Chapter will explain the core concepts of SVMs, how to use them, and how they work.
Linear SVM Classification
The fundamental idea behind SVMs is best explained with some pictures.
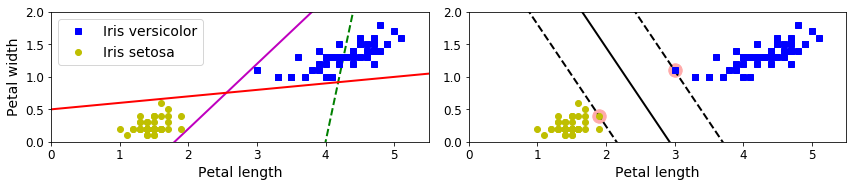
Figure 5-1 shows part of the iris dataset that was introduced at the end of Chapter 4.
The two classes can clearly be separated easily with a straight line (they are linearly separable).
The left plot shows the decision boundaries of three possible linear classifiers.
The model whose decision boundary is represented by the dashed line is so bad that it does not even separate the classes properly.
The other two models work perfectry on this training set, but their decision boundaries come so close to the instances that these models will probably not perform as well on new instances.
In contrast, the solid line in the plot on the right represent the decision boundaries of an SVM classifier;
this line not only separates the two classes but also stays as far away from the closest training instanses as possible.
You can think of an SVM classifier as fitting the widest possible street (represented by the parallel dashed lines) between the classes.
This is called large margin classification.
Notice that adding more training instances "off the street" will not affect the decision boundary at all:
it is fully determined (or "supported") by the instances located on the edge of the street.
These instances are called the support vectors (they are circled in Figure 5-1).
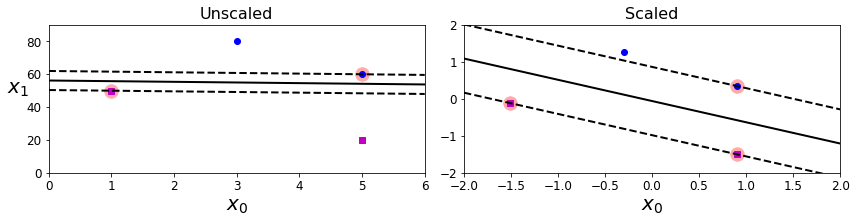
SVMs are sensitive to the feature scale, as you can see in Figure 5-2:
in the left plot, the vertical scale is much larger than the horizontal scale, so the widest possible street is close to horizontal.
After feature scaling (e.g., using Scikit-Learn's StandardScaler), the decision boundary in the right plot looks much better.
Soft Margin Classification
If we strictly impose that all instances must be off the street and on the right side, this is called hard margin classification.
There are two main issues with hard margin classification.
First, it only works if the data is linearly separable.
Second, it is sensitive to outliers.
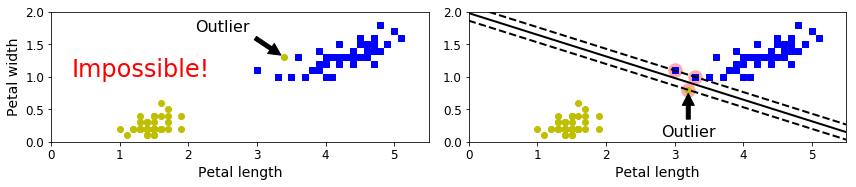
Figure 5-3 shows the iris dataset with just one additional outlier:
on the left, it is impossible to find a hard margin;
on the right, the decision boundary ends up very different from the one we saw in Figure 5-1 without the outlier, and it will probably not generalize as well.
To avoid these issues, use a more flexible model.
The objective is to find a good balance between keeping the street as large as possible and limiting the margin violations (i.e., instances that end up in the middle of the street or even on the wrong side).
This is called soft margin classification.
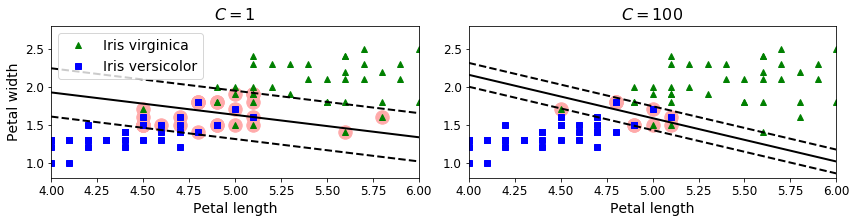
When creating an SVM model using Scikit-Learn, we can specify a number of hyperparameters.
C is one of those hyperparameters.
If we set it to a low value, then we end up with the model on the left of Figure 5-4.
With a high value, we get the model on the right.
Margin violations are bad.
It's usually better to have few of them.
However, in this case the model on the left has a lot of margin violations but will probably generalize better.
If your SVM model is overfitting, you can try regularlizing it by reducing C.
The following Scikit-Learn code loads the iris dataset, scale the features, and then trains a linear SVM model (using the linear SVC class with C=1 and the hinge loss function, described shortly) to detect Iris virginica flowers.
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm impoet LinearSVC
iris = datasets.load_iris( )
X = iris["data"][ : , (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64) # iris virginica
svm_clf = Pipeline([
("scaler", StandardScaler( )),
("linear_svc", LinearSVC(C=1, loss="hinge")),
])
svm_clf.fit(X, y)
The resulting model is represented on the left in Figure 5-4.
Then, as usual, you can use the model to make predictions:
array([1.])
Unlike Logistic Regression classifiers, SVM classifiers do not output probabilities for each class.
Instesd of using the Linear SVC class, we could use the SVC class with a linear kernel.
When creating the SVC model, we would write SVC(kernel="linear", C=1).
Or we could use the SGDClassifier class, with SGDClassifier(loss="hinge", alpha=1/(m*C)).
This applies regular Stochastic Gradient Descent (see Chapter 4) to train a linear SVM classifier.
It does not converge as fast as the Linear SVC class, but it can be useful to handle online classification tasks or huge datasets that do not fit in memory (out-of-core training).
The LinearSVC class regularizes the bias term, so you should center the training set first by subtracting its mean.
This is automatic if you scale the data using the StandardScaler.
Also make sure you set the loss hyperparameter to "hinge", as it is not the default value.
Finally, for better performance, you should set the duel hyperparameter to False, unless there are more features than training instances (we will discuss duality later in the chapter).
Nonlinear SVM Classification
SVMで良い結果を得たという情報に出会うまで、ペンディング!
そういう事例に遭遇して、勉強不足と感じたら、学習再開!


