Chapter 10 Introduction to Artificial Neural Networks with Keras
Hands-On Machine Learning with Scikit-Learn, Keras & Tensorflow 2nd Edition by A. Geron
From Biological to Artificial Neurons
Biological Neurons
Logical Computations with Neurons
The Perceptron
Scikit-Learn provides a Perceptron class that implements a single-TLU (threschold logic unit) netwoek. It can be used pretty much as you would expect - for example, on the iris dataset (introduced in Chapter 4):
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:, (2, 3)] # petal length, petal width
y = (iris.target == 0).astype(np.int)
per_clf = Perceptron(max_iter=1000, tol=1e-3, random_state=42)
per_clf.fit(X, y)
y_pred = per_clf.predict(2, 0.5)
y_pred
array([1])

The Multilayer Perceptron and Backpropagation
An MLP is composed of one (passthrough) input layer,
one or more layers of TLUs, called hidden layers,
and one final layer of TLUs called the output layer.
The layers close to the input layer are usually called the lower layers, and the ones close to the outputs are usually called the upper layers.
このinput layer : lower layers, outoput layer : upper layersの表現、
混乱の元になることがあるので、要注意。
この通りに図示、すなわち入力層を下側に、出力層を上側に書かれているものもあれば、逆方向の模式図もあれば、左側に入力層というのもある。
慣れれば、文章と図面が逆方向を指していてもなんら問題は無いのだが、
初心者の頃には、入力層側と出力層側のどちらを指しているのかわからず、
きついな、と思ったことがある。
Every layer except the output layer includes a bias neuron
and is fully connected to the next layer.
When an ANN contains a deep stack of a hidden layers,
it is called a deep neural network (DNN).
The field of Deep Learning studies DNNs, and more generally models containing deep stacks of computations.
For many years researchers struggled to find a way to train MLPs, without success.
But in 1986, David Rumelhart, Geoffrey Hinton, and Ronald Williams published a groundbreaking paper that introduced the backpropagation training algorithm, whichi is still used today.
In short, it is Gradient Descent (introduced in Chapter 4) using an efficient technique for computing the gradients automatically: in just two passes through the network (one forward, one backward), the backpropagation algorithm is able to compute the gradient of the network's error with regard to every single model parameter.
In other words, it can find out how each connection weight and each bias term should be tweaked in order to reduce the error.
Once it has these gradients, it just performs a regular Gradient Descent step, and the whole process is repeated until the network converges to the solution.
Let's run through this algorithm in a bit more detail:
・It handles one mini-batch at a time (for example, containing 32 instances each), and it goes through the full training set multiple times. Eaxh pass is called an epoch.
・Each mini-batch is passed to the network's input layer, which sends it to the first hidden layer. The algorithm then computes the output of all the neurons in this layer (for every instance in the mini-batch). The result is passed on to the next layer, its output is computed and passed to the next layer, and so on untill we get the output of the last layer, the output layer. This is the forward pass: it is exactly like making predictions, except all intermediate results are preserved since they are needed for the backward pass.
・Next, the algorithm measures the network's output error (i.e., it uses a loss function that compares the desired output and the actual output of the network, and returns some measure of the error.
・Then it computes how much each output connection contributed to the error. This is done analytically by applying the chain rule (perhaps the most fundamental rule in calculus), which makes this step fast and precise.
・The algorithm then measures how much of these error contributions came from each connection in the layer below, again using the chain rule, working backward until the algorithm reaches the input layer. As explained earlier, this reverse pass efficiently measures the error gradient across all the connection weights in the network by propagating the error gradient backward through the network (hence the name of the algorithm).
・Finally, the algorithm performs a Gradient Descent step to tweak all the connection weights in the network, using the error gradients it just computed.
This algorithm is so important that it's worth summarizing it again:
for each training instance, the backpropagation algorithm first makes a prediction (forward pass) and measures the error, then goes through each layer in reverse to measure the error contribution from each connection (reverse pass), and finally tweaks the connection weights to reduce the error (Gradient Descent step).
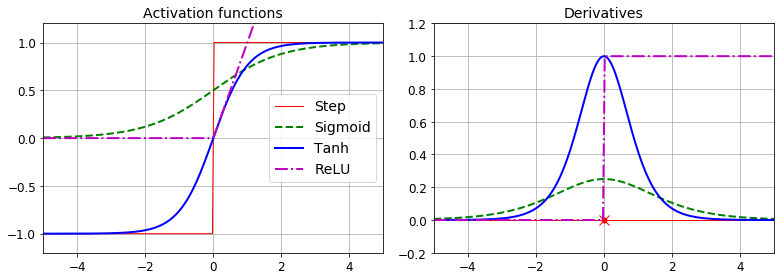
step function
logistic (sigmoid) function: σ(z) = 1 / (1 + exp(-z))
hyperbolic tangent function: tanh(z) = 2σ(2z) - 1
rectified linear unit function: ReLU(z) = max(0, z)
The popular activation functions and their derivatives are represented in Figure 10-8.
But weit!
Why do we need activation functions in th first place?
Well, if you chain several linear functions, all you get is a linear transformation.
For examaple, if f(x) = 2x +3 and g(x) =5x -1, then chaining these two linear functions gives you another linear function: f(g(x)) = 2(5x - 1) + 3 = 10x +1.
So if you don't have some nonlineality between lauers, then even a deep stack of layers is equivalent to a single layer, and you can't solve very complex problems with that.
Conversely, a large enough DNN with nonlinear activations can theoretically approximate any continuous function.
Regression MLPs
First, MLPs can be used for regression tasks.
If you want to predict a single value (e.g., the price of a house, given many of its features), then you just need a single output neuron: its output is the predicted value.
例:住宅の場所、平均収入、建物あたりの部屋数、築年数などのデータを入力して、住宅価格を予測(推定)する場合
For multivariate regression (i.e., to predict multiple values at once), you need one output neuron per output dimension. For example, to locate the center of an object in an image, you need to predict 2D coordinates, so you need two output neurons. If you also want to place a bounding box around the object, then you need two more numbers; the width and the height of the object. So, you end up with four output neurons.
例:車載カメラの画像を入力して、車(他車)の位置(重心)と、バウンディングボックス(枠)のサイズ(縦と横)を予測(推定)する場合
In general, when building an MLP for regression, you do not want to use any activation function for the output neurons, so they are free to output any range of value.
If you want to guarantee that the output will always be positive, then you can use the ReLU activation function in the output layer.
Alternatively, you can use the softplus activation function, which is a smooth variant of ReLU: softplus(z) = log(1 + exp(z)). It is close to 0 when z is negative, and close to z when z is positive.
Finally, if you want to guarantee that the prediction will fall within a given range of values, then you can use the logistic function or the hyperbolic tangent, and then scale the lables to the appropriate range: 0 to 1 for the logistic function and -1 to 1 for the hyperbolic tangent.
回帰問題は、数値をそのまま出力する場合は、出力層の活性化関数は不要。
出力値として正の数にしたい場合はReLUかsoftplusを用いる。
さらに、出力をある数値範囲に収めたい場合は、logisticまたはtanhを用いる。
The loss function to use during training is typically the mean squared error, but if you have a lot of outliers in the training set, you may prefer to use the mean absolute error instead. Alternatively, you can use the Huber loss, which is a combination of both.
損失関数は、MSEまたはMAE/Huber。
Table 10-1. Typical regression MLP architecture
Hyperparameter Typical value
# input neurons One per input feature (e.g., 28 x 28 = 784 for MNIST
# hidden layers Depends on the problem, but typically 1 to 5
# neurons per hidden layer Depends on the problem, but typically 10 to 100
# output neurons 1 per prediction dimension
Hidden activation ReLU (or SELU, see Chapter 11)
Output activation None, or ReLU/softplus (if positive outputs) or logistic/tanh (if bounded outputs)
Loss function MSE or MAE/Huber (if outliers)
Classification MLPs
MLPs can also be used for classification tasks.
For a binary classification problem, you just need a single output neuron using the logistic activation function: the output will be a number between 0 and 1, which you can interpret as the estimated probability of the positive class.
The estimated probability of the negative class is equal to one minus that number.
例:テキストデータ(email)を入力して、spamとham(正常)を分類する場合
例:手書き文字画像データを入力して、5と、5以外の数字を分類する場合
MLPs can also easily handle multilabel binary classification tasks (see Chapter 3).
For example, you could have an email classification system that predicts whethere each incoming email is ham or spam, and simultaneously predicts whether it is an urgent or nonurgent.
In this case, you would need two output neurons, both using the logic activation function: the first would output the probability that the email is spam, and the second would output the probability that it is urgent.
例:テキストデータ(email)を入力して、spamかどうかと、緊急かどうかを見分ける場合は、それぞれ別々の出力neuronを設ける。
If each instance can belong oy to a single class, out of three or more possible classes (e.g., classes 0 through 9 for digit image classification), then you need to have one output neuron per class, and you should use the softmax activation function for the whole output layer.
The softmax function (introduced in Chapter 4) will ensure that all the estimated probabilities are between 0 and 1 and that they add up to 1 (whichi is required if the classes are exclusive).
This is called multiclass classification.
例:手書き文字画像データを入力して、0から9までの数字を分類する場合
Table 10-2. Typical classification MLP architecture
Hyperparameter Binary classification Multilable binary classification Multiclass classification
input and hidden layers ------------------------ same as regression ------------------------
# output neurons 1 1 per lable 1 per class
Output layer activation Logistic Logistic Softmax
Loss function Closs entropy Cross entropy Closs entropy
Implementing MLPs with Keras
Installing TensorFlow 2
Building an Image Classifier Using the Sequential API
First, we need to load a dataset. In this chapter we will tackle Fashon MNIST, which is a drop-in replacement of MNIST (introduced in Chapter 3). It has the exact same format as MNIST (70,000 grayscale images of 28 x 28 pixels each, with 10 classes), but the images represent fashion items rather than handwritten digits, so each class is more diverse, and the problem turns out to be significantly more challenging than MNIST. For example, a simple linear model reaches about 92% accuracy on MNIST, but only about 83% on Fashion MNIST.
Using Keras to load the dataset
fashion_mnist = keras.datasets.fashion_mnist
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data( )
When loading MNIST or Fashion MNIST using Keras rather than SciKit-Learn, one important differenve is that every image is represented as a 28 x 28 array rather than a 1D array of size 784. Moreover, the pixel intensities are represented as integers (from 0 to 255) rather than floats (from 0.0 to 255.0).
X_train_full.shape
(60,000, 28, 28)
X_train_full.dtype
dtype( 'unit8' )
Note that the dataset is already split into a training set and a test set, but there is no validation set, so we'll create one now.
Additionally, since we are going to train the neural network using Gradient Descent, we must scale the input features.
入力データのスケーリングは、必ずチェックすること!
For simplicity, we'll scale the pixel intensities down to the 0-1 range by dividing them by 255.0 (this also converts them to floats):
X_valid, X_train = X_train_full[ :5000] / 255.0, X_train_full[5000: ] / 255.0
y_valid, y_train = y_train_full[ :5000], y_train_full[5000: ]
With MNIST, when the lable is equal to 5, it means that the image represents the handwritten digit 5. Easy. For Fashion MNIST, however, we need the list of class names to know what we are dealing with:
手書き数字の認識のラベルは、0, 1, 2, 3, 4, 5, 6, 7, 8, 9 である。
ファッションアイテムの画像認識のラベルは、品物の名前である。
class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat",
"Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]
class_names[y_train[0]]
'Coat'
Creating the model using the Sequential API
Now let's build the neural network! Here is a classification MLP with two hidden layers.
model = keras.models.Sequential( )
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu"))
model.add(keras.layers,Dense(100, activation="relu"))
model.add(keras.layers.Dense(10, activation="softmax"))
Let's go through this code line by line:
・The first line creates a sequential model. This is the simplest kind of Keras model for neural networks that are just composed of a single stack of layers connected sequentially. This is called the Sequential API.
・Next, we buid the firstlayer and add it to the model. It is a flatten layer whose role is to convert each input image into 1D array: if it receives input data X, it computes X.reshape(-1, 1).
This layer does not have any parameters; it is just there to do some simple preprocessing.
Since it is the first layer in the model, you should specify the input_shape, which doesn't include the batch size, only the shape of the instances.
Alternatively, you could add a keras.layers.Inputlayer as the first layer, setting input_shape=[28, 28]
・Next we add a Dense hidden layer with 300 neurons.
It will use the ReLU activation function.
Each Dense layer manages its own weight matrix, containing all the connection weights between the neurons and their inputs.
It also manages a vector of bias terms (one per neuron).
When it receives some input data, it computes Equation 10-2.
Equation 10-2: hw,b(X) = Φ(XW + b):
weight matrix w, bias bector b, matrix of input features X, activation function Φ
・Then we add a second Dense hidden layer with 100 neurons, also using the ReLU activation function.
・Finally, we add a Dense output layer with 10 neurons (one per class), using the softmax activation function (because the classes are exclusive).
Specifying activation="relu" is equivalent to specifying activation=keras.activations.relu. Other activation functions are available in the keras.activations package.
次の表現もOK
Instead of adding the layers one by one as we just did, you can pass a list of layers when creating the Sequential model.
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="relu"),
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
The model's summary( ) method displays all the model's layers, including each layer's name (which is automatically generated unless you set it when creating the layer), its output shape (None means the batch size can be anything), and its number of parameters.
The summary ends with the total number of parameters, including trainable and non-trainable parameters.
Here we only have trainable parameters (we will see examples of non-trainable parameters in Chapter 11).
model.summary( )
Model: "sequential"
_________________________________________________________________
Layer (type) utput Shape Param #
=======================================
flatten (Flatten) (None, 784) 0
_________________________________________________________________
dense (Dense) (None, 300) 235500
_________________________________________________________________
dense_1 (Dense) (None, 100) 30100
_________________________________________________________________
dense_2 (Dense) (None, 10) 1010
=======================================
Total params: 266,610
Trainable params: 266,610
Non-trainable params: 0
_________________________________________________________________
Note that Dense layer often have a lot of parameters.
For example, the first hidden layer has 784 x 300 connection weights, plus 300 bias terms, which adds up to 235,500 parameters!
This gives the model quite a lot of flexibility to fit the training data, but it also means that the model runs the risk of overfitting, especially when you do not have a lot of training data.
We will come back to this later.
You can easily get a model's list of layers, to fetch a layer by its index, or you can fetch it by name.
model.layers
[<tensorflow.python.keras.layers.core.Flatten at 0x12c15d588>,
<tensorflow.python.keras.layers.core.Dense at 0x149938fd0>,
<tensorflow.python.keras.layers.core.Dense at 0x149b198d0>,
<tensorflow.python.keras.layers.core.Dense at 0x149b19be0>]
hidden1 = model.layers[1]
hidden.name
'dense'
model.get_layer('dense') is hidden
True
All the parameters of a layer can be accessed using its get_weights( ) and set_weights( ) methods.
For a Dense layer, this includes both the connection weights and the bias terms:
weights, biases = hidden1.get_weights( )
weights
array([[ 0.02448617, -0.00877795, -0.02189048, ..., -0.02766046,
0.03859074, -0.06880391],
...,
[-0.06022581, 0.01577859, -0.02585464, ..., -0.00527829,
0.00272203, -0.06793761]], dtype=float32)
weights.shape
(784, 300)
biases
array([0., 0., 0., 0., 0., 0., 0., 0., 0., ..., 0., 0., 0.], dtype=float32)
biases.shape
(300, )
こういう情報は、レイヤーモデルを誰でも簡単に作れる昨今では、特に重要だと思う。
膨大な数の数値が入っているだけなんだと、実感することができる。
Notice that the Dense layer initialized the connection weights randomly (which is needed to break symmetry, as we discussed earlier), and the biases were initialized to zeros, which is fine.
If you ever want to use a different initialization method, you can set kernel_initializer (kernel is another name for the matrix of connection weights) or bias_initializer when creating the layer.
We will discuss initializers further in Chapter 11, but if you want the full list, see http://keras.io/initializers/.
Compiling the model
After a model is created, you must call its compile( ) method to specify the loss function and the optimizer to use.
Optionally, you can specify a list of extra metrics to compute during training and evaluation.
model.compile(loss="sparse_categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"])
This code requires some explanation.
First, we use the "sparse_categorical_crossentropy" loss because we have sparse lables (i.e., for each instance, there is just a target class index, from 0 to 9 in this case), and the classes are exclusive.
If instead we had one target probability per class for each instance (such as one-hot vectors, e.g. [0., 0., 0., 1., 0., 0., 0., 0., 0., 0.] to represent class 3), then we would need to use the "categorical_crossentropy" loss instead.
If we were doing binary classification (with one or more binary lables), then we would use the "sigmoid" (i.e., logistic) activation function in the output layer instead of the "softmax" activation function, and we would use the "binary_crossentropy" loss.
If you want to convert sparse lables (i.e., class indices) to one hot vector lables, use the keras.utils.to_categorical( ) function.
To go the other way round, use the np.argmax( ) function with axis=1.
Regarding the optimizer, "sgd" means that we will train the model using simple Stochastic Gradient Descent.
In other words, Keras will perform the backpropagation algorithm described earlier (i.e., reverse-mode autodiff plus Gradient Descent).
We will discuss more efficient optimizers in Chapter 11 (they improve the Gradient Descent part, not the autodiff).
When using the SGD optimizer the SGD optimizer, it is impoetant to tune the learning rate. So, you will generally want to use optimizer=keras.optimizers.SGD(lr=???) to set the learning rate, rather than optimizer="sgd", which defaults to lr=0.01.
Finally, since this is a classifier, it's useful to measure its "accuracy" during training and evaluation.
Training and evaluating the model
5月25日:飛ばし読みしてわかったこと。このテキストは順番に読んでも難しく、飛ばし読みはさらに難しい。とはいえ、順に読むのが苦痛になると、それこそ、進めなくなるので、このまま、興味に従って、飛ばし読みしていく。
Now the model is ready to be trained.
For this we simply need to call its fit( ) method:
history = model.fit(X_train, y_train,
epochs=30,
validation_data=(X_valid, y_valid) )
Train on 55000 samples, validate on 5000 samples
Epoch 1/30
55000/55000 [==============================] - 3s 62us/sample - loss: 0.7217 - accuracy: 0.7661 - val_loss: 0.4972 - val_accuracy: 0.8366
Epoch 2/30
55000/55000 [==============================] - 3s 51us/sample - loss: 0.4839 - accuracy: 0.8323 - val_loss: 0.4459 - val_accuracy: 0.8482
...............................................................................................................................................
Epoch 28/30
55000/55000 [==============================] - 3s 57us/sample - loss: 0.2331 - accuracy: 0.9165 - val_loss: 0.2981 - val_accuracy: 0.8920
Epoch 29/30
55000/55000 [==============================] - 3s 56us/sample - loss: 0.2289 - accuracy: 0.9176 - val_loss: 0.2959 - val_accuracy: 0.8930
Epoch 30/30
55000/55000 [==============================] - 3s 51us/sample - loss: 0.2255 - accuracy: 0.9183 - val_loss: 0.3004 - val_accuracy: 0.8926
こんな感じで計算が進む。
We pass it the input features (X_train) and the target classes (y_train), as well as the number of epochs to train (or else it would default to just 1, which would definitely not be enough to converge to a good splution).
We also pass a validation set : validation_data=(X_valid, y_valid)(this is optional).
オプションと書いてあるが、validation setは、必須である。
Keras will measure the loss and the extra metrics on this set at the end of each epoch, which is very useful to see how well the model really performs.
If the performance on the training set is much better than on the validation set, your model is probably overfitting the training set (or there is a bug, such as a data mismuch between the training set and the validationset).
fashion MNISTのデータベースをロードして、
X_train_full, y_train_fullとX_test, y_testに分けて、
さらに、X_train_full, y_train_fullを、X_train, y_trainと X_valid, y_validとに分けて、
多層ニューラルネットワークのモデルを作って、
そのモデルをコンパイルして、
そのモデルを訓練した。
15行にも満たない行数で、fashion MNISTのデータを使って、約27万個のパラメータを有する多層ニューラルネットワークモデルを構築し 、訓練することによって、約89%の確からしさで分類出来るモデルを手にすることができた。
And that's it!
The neural network is trained.
At each epoch during training, Keras displays the number of instances processes so far (along with a progress bar), the mean training time per sample, and the loss and accuracy (or any other extra metrics you asked fore) on both the training set and the validation set.
You can see that the training loss went down, which is a good sign, and the validation accuracy reached 89.26% after 30 epochs.
That's not too far from the training accuracy (91.92%), so there does not seem to be much overfitting going on.
If the training set was very skewed, with some classes being overrepresented and others underrepresented, it would be useful to set the class_weight argument when calling the fit( ) method, which would give a larger weight to underrepresented classes and a lower weight to overrepresented classes.
These weights would be used by Keras when computing the loss.
If you need per-instance weights, set the sample_weight argument (if both class_weight and sample_weight are provided, Keras multiples them).
Per-instance weights could be useful if some instances were labled by experts while others were labled using a crowdsourcing platform:
you might want to give more weight to the former.
You can also provide sample weights (but not class weights) for the validation set by adding them as a third item in the validation_data tuple.
信頼性の高いラベル付きデータに対しては、高い重みを与える。
The fit( ) method returns a History object containing the training parameters (history.params), the list of epochs it went through (history.epoch), and most importantly a dictionary (history.history) containing the loss and extra metrics it measured at the end of each epoch on the training set and on the validation set (if any).
If you use this dictionary to create a pandas DataFrame and call its plot( ) method, you get the learning curves shown in Figure 10-12:
import pandas as pd
import matplotlib.pyplot as plt
pd.DataFrame(history.history).plot(figsize=(8.5))
plt.grid(True)
plt.gca( ).set_ylim(0, 1) # set the vetical range to [0 - 1]
plt.show( )
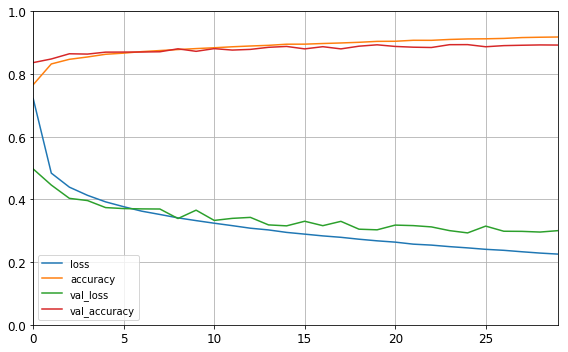
You ca see that both the training accuracy and the validation accuracy steadily increase during training, while the training loss and the validation loss decrease.
Good!
Moreover, the the validation cueves are close to the training curves, which means that there is not too much overfitting.
In this particular case, the model looks like it performed better on the validation set than on the training set at the beginning of training.
But that's not the case:
indeed, the validation error is computed at the end of each epoch, while the training error is computed using a running mean during each epoch.
So the training curve should be shifted by half an epoch to the left.
If you do that, you will see that the training and validation curves overlap aimost perfectry at the beginning of the training.
trainingの初期に、training setよりもvalidation setの方が、lossが小さくaccが大きいのが不思議だったが、こういうことだったのか。
training setはtrainingに用いられ、validation setはvalidationに用いられる。
蛇足かもしれないが、モデルのtrainingすなわち、パラメーターの最適化はtraining setを用いて行われ、validation setは、training中のモデルの性能を測るためにのみ、用いられる。
The training set performance ends up beating the validation performance, as is generally the case when you train for long enough.
You can tell that the model has not quite converged yet, as the validation loss is still going down, so you should probably continue training.
It's as simple as calling the fit( ) method again, since Keras just continues training where it left off (you should be able to 89% validation accuracy).
追加で計算できる機能は、非常に便利。その理由は、実際に使ってみるとすぐわかる。
とにかく、ディープラーニングは、計算時間が長いのだ。
If you are not satisfied with the performance of your model, you should go back and tune the hyperparameters.
The first one to check is the leraning rate.
If that doesn't help, try another optimizer (and always retune the learning rate after changing any hyperparameter).
If the performance is still not great, then try tuning model hyperparameters such as the number of layers, the number of neurons per layer, and the types of activation functions to use for each hidden layer.
You can also try tuning other hyperparameters, such as the batch size (it can be set in the fit( ) method using the batch_size argument, which defaults to 32).
We will get back to hyperparameter tuning at the end of this chapter.
Once you are satisfied with your model's validation accuracy, you should evaluate it on the test set to estimate the generalization error before you deploy the model to production.
You can easily do this using the evaluate( ) method (it also supports several other arguments, such as batch_size and sample_weight; please check the documentation for more details):
model.evaluate(X_test, y_test)
10000/10000 [==============================] - 0s 31us/sample - loss: 0.3343 - accuracy: 0.8857
[0.33426858170032503, 0.8857]
As we saw in Chapter 2, it is common to get slightly lower performance on the test set than on the validation set, because the hyperparameters are tuned on the validation set, not the test set (however, in this example, we did not do any hyperparameter tuning, so the lower accuracy is just bad luck).
Remember to resist the temptation to tweak the hyperparameters on the test set, or else your estimate of the generalization error will be too optimistic.
Using the model to make predictions
Next, we can use the model's predict( ) method to make predictions on new instances.
Since we don't have actual new instances, we will just use the first three instances of the test set:
X_new = X_test[ :3]
y_proba = model.predict(X_new)
y_proba.round(2)
array([[0. , 0. , 0. , 0. , 0. , 0.02, 0. , 0.02, 0. , 0.96],
[0. , 0. , 0.98, 0. , 0.02, 0. , 0. , 0. , 0. , 0. ],
[0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ]],
dtype=float32)
クラス0からクラス9までの確率が表示されている。
確率が最も高いのは、class 9, class 2, class1である。
クラスを直接出力するには、predict_classes( ) methodを使う。
y_pred = model.predict_classes(X_new)
y_pred
array([9, 2, 1])
np.array(class_names)[y_pred]
array(['Ankle boot', 'Pullover', 'Trouser'], dtype='<U11')
Building a Regression MLP Using the Sequential API
Let's switch to the California housing problem and tackle it using a regression neural network.
For simplicity, we will use Scikit-Learn's fetch_california_housing( ) function to load the data.
This dataset is simpler than the one used in Chapter 2, since it contains only numerical features (there is no ocean_proximity feature), and there is no missing value.
After loading the data, we split it into a training set, a validation set, and a test set, and we scale all the feature.
from sklearn.dataset import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing( )
X_trsin_full, X_test, y_train_full, y_test = train_test_split(
housing.data, housing.target)
X_train, X_valid, y_train, y_valid = train_test_split)
X_train_full, y_train_full)
scaler = StandardScaler( )
X_train = scalar.fit_transform(X_train)
X_valid = scaler.transform(X_valid)
X_test = scaler.transform(X_test)
Using the Sequential API to build, train, evaluate, and use a regression MLP to make predictions is quite similar to what we di for classification.
The main differences are the fact that the output layer has a single neuron (since we only want to predict a single value) and uses no activation function, and the loss function is the mean squared error.
Sinse tha dataset is quite noisy, we just use a single hidden layer with fewer neurons than before, to avoid overfitting:
model = keras.models.Sequential([
keras.layers Dense(30, activation="relu", input_shape=X_train.shape[1:]),
keras.layers.Dense(1)
])
model.compile(loss="mean_squared_error", optimizer="sgd")
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
X_new = X_test[ :3] # pretend these are new instances
y_pred = model.predict(X_new)
As you can see, the Sequential API is quite easy to use,
However, although Sequential models are extremely common, it is sometimes useful to build neural networks with more complex topologies, or with multiple inputs or outputs.
For this purpose, Keras offers the Functional API
Building Complex Models Using the Functional API
One example of a nonsequential neural network is a Wide & Deep neural network.
This neural network architechture was introduced in a 2016 paper by Heng-Tze Cheng et al.
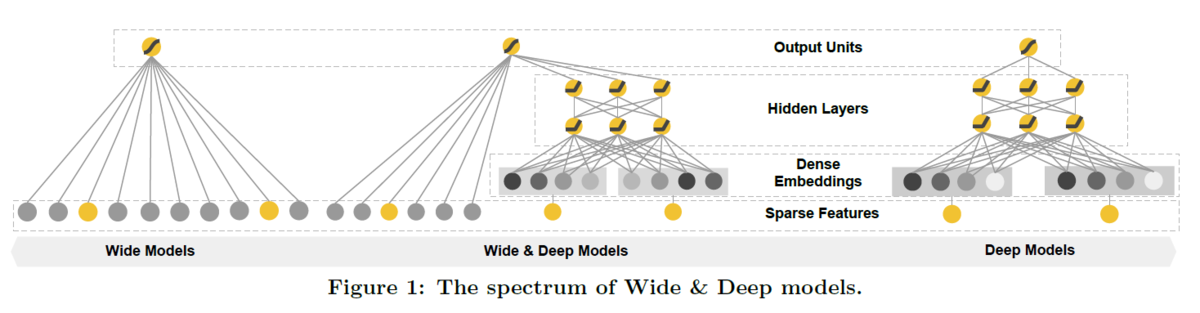
It connects all or part of the inputs directly to the output layer, as shown in Figure 10-14.
This architecture makes it possible for the neural network to learn both deep patterns (using the deep path) and simple rules (through the short path).
In contrast, a regular MLP forces all the data to flow through the full stack of layers, thus, simple patterns in the data may be end up being distorted by this sequence of transformations.
Let's build such a neural network to tackle the California housing problem:
input_ = keras.layers.Input(shape=X_train.shape[1:])
hidden1 = keras.layers.Dense(30, activation="relu")(input_)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_, hidden2])
output = keras.layers.Dense(1)(concat)
model = keras.models.Model(inputs=[input_], outputs=[output])
Let's go through each line of this code
・First, we need to create an Input object. (the name "input_" is used to avoid overshadowing Python's built-in input( ) function.)
This is a specification of the kind of input the model will get, including its shape and dtype.
A model may actually have multiple inputs, as we will see shortly.
・Next, we create a Dense layer with 30 neurons, using the ReLU activation function.
As soon as it is created, notice that we call it like a function, passing it the input.
This is why this is called the Functional API.
Note that we are just telling Keras how it should connect the layers together; no actual data is being processed yet.
・We then create a second hidden layer, and again we use it as a function.
Note that we pass it the output of the first hidden layer.
・Next, we create a Concatenate layer, and once again we immediately use it like a function, to concatenate the input and the output of the second hidden layer.
You may prefer the keras.layers.concatenate( ) function, which creates a Concatenate layer and immediately calls it with the given inputs.
・Then we create the output layer, with a single neuron and no activation function, and we call it like a function, passing it the result of the concatenation.
・Lastly, we create a Keras Model, specifying which inputs and outputs to use.
Once you have built the Keras model, everything is exactly like earlier, so there's no need to repeat it here: you must compile the model, train it, evaluate it, and use it to make predictions.
But what if you want to send a subset of the features through the wide path and a different subset (possibly overlapping) through the deep path (see Figure 10-15)?
In this case, one solution is to use multiple inputs.
For example, suppose we want to send five features through the wide path (feature 0 to 4), and six features through the deep path (feature 2 to 7):
input_A = keras.layers.Input(shape=[5], name="wide_input")
input_B = keras.layers.Input(shape=[6], name="deep_input")
hidden1 = keras.layers.Dense(30, activation="relu")(input_B)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
output = keras.layers.Dense(1, name="output")concat)
model = keras.Model(inputs=[input_A, input_B], outputs=[output])
The code is self-explanatory.
You should name at least the most important layers, especially when the model gets a bit complex like this.
Note that we specified inputs=[input_A, input_B] when creating the model.
Now we can compile the model as usual, but when we call the fit( ) method, instead of passing a single input matrix X_train, we must pass a pair of matrices (X_train_A, X_train_B): one per input.
The same is true for X_valid, and also for X_test and X_new when you call evaluate( ) or predict( ):
model.compile(loss="mse",
Using the Subclassing API to Build Dynamic Models
Saving and Restoring a Model
2020年8月20日の時点においても、これが使えていない。
Using Callbacks
Using TensorBoard for Visualization
Fine-Tuning Neural Network Hyperparameters
Number of Hidden Layers
Number of Neurons per Hidden Layer
Learning Rate, Batch Size, and Other Hyperparameters
Exercises


